Breaking Down the Basics: Understanding Order of Operations
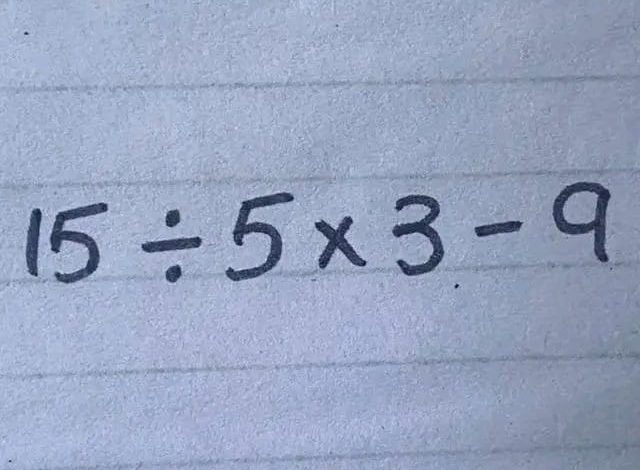
Breaking Down the Basics: Understanding Order of Operations
Introduction:
Mathematics is a universal language spoken through numbers and operations, but its clarity can depend heavily on understanding foundational rules such as the order of operations. The expression in the image – “15 ÷ 5 × 3 – 9” – serves as a perfect canvas to explore these fundamental principles, which ensure that regardless of where you are in the world, the way you solve mathematical problems remains consistent.
Body: Exploring the Order of Operations:The order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right)), dictates the sequence in which parts of a mathematical expression should be solved. This rule prevents ambiguity in mathematical expressions.
- Parentheses – Complete all calculations inside parentheses first.
- Exponents – Solve expressions involving exponents or powers next.
- Multiplication and Division – These operations are treated equally and are carried out from left to right.
- Addition and Subtraction – Like multiplication and division, these operations are processed from left to right.
Application to the Provided Expression:Applying these rules to the expression in the image:
- The expression given is “15 ÷ 5 × 3 – 9”.
- There are no parentheses or exponents, so we proceed with division and multiplication from left to right.
- First, divide 15 by 5, which equals 3.
- Next, multiply 3 by 3, resulting in 9.
- Finally, subtract 9 from 9, which equals 0.
Misconceptions and Errors: A common error in solving such expressions arises when individuals overlook the rule that multiplication and division are of equal precedence and should be processed sequentially from left to right. Ignoring this can lead to significantly different and incorrect results.
Conclusion: The order of operations is crucial in mathematics as it provides a clear protocol for solving expressions in a systematic and universally understandable way. The expression “15 ÷ 5 × 3 – 9” is not just a test of arithmetic but also an illustration of why mathematical conventions like PEMDAS are essential. Understanding and applying these rules can prevent errors and ensure accuracy whether one is solving simple calculations or tackling complex algebraic expressions.
This discussion not only reinforces the importance of the order of operations but also encourages a meticulous approach to mathematical problem-solving, emphasizing clarity, accuracy, and the universal nature of mathematical principles.